Analisis Distribusi Tegangan Pada Pipa Reducer
Akibat Beban Momen Lentur Dengan
Menggunakan Metode Elemen Hingga
Gatot Santoso*
Jurusan Teknik Mesin
Fakultas Teknik Universitas Pasundan
(gambar-gambar yang tidak tampil, dapat diminta dengan
menghubungi penulis di millist kopertis-iv)
Abstrak
Makalah ini mengetengahkan hasil perhitungan tegangan
yang terjadi pada pipa reducer akibat beban momen lentur (in-plane bending
moment) dengan menggunakan program paket finite element MECHANICA dan SAP90.
Keluaran dari kedua program paket tersebut divisualisasikan dalam bentuk
kurva tegangan vs lokasi, yang selanjutnya kedua keluaran dibandingkan
satu dengan lainnya.
Kata kunci : pipa reducer, distribusi tegangan, metode
elemen hingga, momen lentur.
I. TABEL NOTASI
d = diameter nominal pipa kecil
D = diameter nominal pipa besar
M = momen lentur
t = tebal dinding pipa kecil
T = tebal dinding pipa besar
? = sudut kemiringan pipa reducer
? = tegangan normal
? = tegangan geser
II. PENDAHULUAN
Tegangan pada perpotongan bagian kerucut dan bagian silinder
dari bejana tekan telah diteliti oleh Boardman (1960), Langer (1971), Zaremba
(1959), John dan Orange (1961) dengan memakai metode analitik. Roark &
young (1976) dan Badnar (1981) menuliskan semua pekerjaan mereka didalam
buku yang disusunnya
Untuk setiap komponen sistem perpipaan ada 5 variabel
utama yang mempengaruhi, yaitu : (1) dimensi dari pipa reducer (D, d, T,
t, tc, ?), (2) macam beban yang dikenakan, (3) macam tumpuan, (4) cara
pembuatan pipa reducer, dan (5) material reducer.
Makalah ini menyajikan perhitungan numerik distribusi
tegangan sepanjang pipa reducer dengan memakai paket program MECHANICA
dan SAP90, beban yang dikenakan berupa momen-lentur (in-plane bending moment).
III. PROSEDUR
III.1. MODEL FISIK
Sebagai model fisik pipa reducer dipilih pipa besar dengan
diameter nominal 8 inch dengan tebal dinding pipa 0,1 inch dan panjang
pipa 20 inch, sedangkan pipa kecil dengan diameter nominal 4 inch dengan
tebal dinding pipa 0,1 inch dan panjang pipa 20 inch, dan bagian kerucut
mempunyai sudut kemiringan 450 dengan tebal dinding pipa 0,1 inch, sebagaimana
digambarkan pada sket di bawah ini.
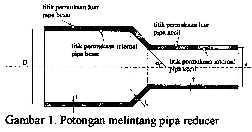
III.2. MODEL FINITE ELEMENT
Ada dua model finite element yang dibuat, yaitu pertama
model untuk program paket MECHANICA dan kedua model untuk program paket
SAP90.
Pada model finite element yang pertama, model disusun
dalam 3 tahap. Tahap pertama adalah menentukan titik nodal pada pipa reducer
seperti digambarkan pada Gambar 2.
Titik nodal, yang dipresentasikan oleh lingkaran-lingkaran kecil, pada
model finite element dari pipa reducer berjumlah empat puluh buah yang
semuanya membentuk tiga puluh enam buah elemen. Tahap kedua adalah membagi
duabelas elemen menjadi masing masing 5 elemen kecuali elemen bagian kerucut
dibagi menjadi 2 elemen (Gambar 3). Tahap ketiga adalah membegi semua elemen
hasil kedua tahap terdahulu masing-masing menjadi seratus elemen yaitu
dengan menambahkan sembilan puluh enam nodal tambahan pada setiap elemen.
Pembagian elemen tersebut dapat dilakukan oleh MECHANICA secara automatis.
Pembentukan model finite element yang kedua, titik nodal ditentukan
pada pipa reducer seperti digambarkan pada Gambar 4.
III.3. MOMEN LENTUR DAN TUMPUAN PIPA REDUCER
Momen lentur dimodelkan dengan gaya-gaya yang terdistribusi secara
linear dan bertitik tangkap pada setiap nodal diujung pipa reducer (Gambar
5). Gaya-gaya tersebut mempunyai resultan momen lentur sebesar 10995 lb.
In.
Percabangan pipa ditumpu dengan tumpuan sederhana (Gambar 6)
IV. KELUARAN HASIL PERHITUNGAN DENGAN METODE FINITE ELEMENT
MECHANICA menghitung enam buah komponen tegangan ?x,
?y, ?z, ?xy, ?yz, ?xz, tiga tegangan utama ?1, ?2, ?3, perpindahan x, y,
z dan rotasi ?1, ?2, ?3 untuk setiap titik nodal, baik titik nodal yang
dipilih mula mula maupun titik nodal yang ditambahkan secara automatis
oleh MECHANICA.
SAP90 menghitung tiga buah komponen tegangan S11, S22
dan S33, dua tegangan utama Smax dan Smin, perpindahan U(x), U(y), U(z)
dan rotasi R(x), R(y), R(z) untuk setiap titik nodal yang dipilih mula-mula.
Untuk keperluan pemrosesan lebih lanjut, maka ke-enam
komponen teganganpada titik-titik nodal terpilih yang terletak dipermukaan
luar dan internal dibaca, garis Ao-Bo-Co-Do dan AI-BI-CI-DI seperti pada
Gambar 6.
V. PEMROSESAN DATA
Tegangan-tegangan pada garis Ao-Bo-Co-Do dan AI-BI-CI-DI
kemudian digambarkan sebagai kurva tegangan vs. lokasi pada Gambar 7, Gambar
8, Gambar 9 dan Gambar 10.
Gambar 8 : tegangan tangensial dan tegangan meridional
pada titik-titik luar pipa reducer pada garis Ao-Bo-Co-Do untuk kasus pertama
Gambar 9 : tegangan tangensial dan tegangan meridional
pada titik-titik luar pipa reducer pada garis Ao-Bo-Co-Do untuk kasus kedua
Gambar 10 : tegangan tangensial dan tegangan meridional
pada titik-titik internal pipa reducer pada garis Ai-Bi-Ci-Di untuk kasus
pertama
Gambar 11 : tegangan tangensial dan tegangan meridional
pada titik-titik internal pipa reducer pada garis Ai-Bi-Ci-Di untuk kasus
kedua
VI. DISKUSI DAN PENUTUP
Diagram distribusi tegangan hasil perhitungan finite
element dengan menggunakan program paket MECHANICA dan SAP90, untuk setiap
macam tegangan yang sama yang terjadi sepanjang garis-garis pada permukaan
luar dan permukaan internal yang sama, diletakkan pada satu halaman untuk
memudahkan perbandingan.
Secara umum dapat dinyatakan bahwa kurva distribusi tegangan
hasil perhitungan program paket MECHANICA dan program paket SAP90 adalah
sama, perbedaan hanya terlihat dari tegangan maksimum dan tegangan minimum
dimana hasil program paket SAP90 menunjukan harga yang lebih besar.
Maka dapat disimpulkan bahwa pemakaian program paket
yang berbeda untuk perhitungan pipa reducer tidak berpengaruh terhadap
distribusi tegangan, hanya harus diwaspadai tegangan maksimum dan tegangan
minimum yang dihasilkan
UCAPAN TERIMA KASIH
Penelitian ini dibiayai oleh Proyek Peningkatan Penelitian
dan Pengabdian kepada Masyarakat Depdikbud melalui Program HTPP dengan
Kontrak No. 016/HTPP/URGE/1995.
DAFTAR PUSTAKA
1. Boardman, H. C., 1960. “Stress at Junction of
Cone and Cylinder in Tank with Cone Bottoms or Ends,” Pressure Vessel and
Piping Design Collected Paper, ASME, New York.
2. Bednar, Henry, H., 1981,”Pressure Vessel Design Handbook,”
Van Nostrand Reinhold Company, New York.
3. Johns, R. H. and Orange, T. W., 1961, “Theoretical
Elastic Stress Distribution Arising from Discontinuities and Edge Loads
in Several Shell-Type Structures,” NASA Tech. Report R-103.
4. Langer, B. F., 1971, “Design-Stress Basis for Pressure
Vessels,” Exp. Mech. Journal Soc. Exp. Stress Analysis, Vol. 11 No. 1.
5. MECHANICA, 1994, “Model Reference: Structure and Thermal
Release 7,” Rasna Corporation. San Jose, California.
6. Roark, R. J. and Young, W. C., 1975, “Formulas for
Stress and Strain,” Mc. Graw-Hill International Book Company.
7. Wilson, E. L. and Habibullah, A., 1992, “User Manual
SAP90,” Computers & Structures Inc., Berkeley, California.
8. Zaremba, W. A., 1959, “Elastic Intersection at the
Junction of an Assembly of Axi-Symmetris Shells,” Journal Mechanical Engineering
Science, Vol. I, No. 3.
